卫星帆板建模方法及相关性验证

刘广明12 ,骆海涛12 ,于长帅12

(1. 中国科学院沈阳自动化研究所机器人学国家重点实验室,辽宁沈阳 110016;

2. 中国科学院机器人与智能制造创新研究院,辽宁沈阳 110016)

        摘  要:蜂窝材料因其优越的力学性能而被广泛应用于卫星帆板结构中,多采用三明治夹层结构。目前有限元软件无蜂窝夹层单元,建模时大量采用等效算法,尤其当结构比较复杂时,建立与实际帆板力学特性相一致的有限元模型是比较难的,因为诸多因素都会影响到有限元模型的精度。而建模方法的准确性直接关系到仿真结果的正确性,造成有限元模型与真实物理样机产生偏差。通过三明治夹芯理论建立了一种蜂窝板的有限元模型,将有限元模态计算结果与模态试验结果进行相关性分析,计算出模态置信度MAC (Modal Assurance criteria) 来评估模态振型的符合程度。结果表明,所建立的卫星帆板有限元模型具有较高的精度, 仿真计算所采用的建模方法是合适的,为卫星帆板仿真建模指导规范的建立提供了参考。

        关键词:相关性; 蜂窝板; MAc;模态分析;卫星帆板 

        中图分类号:V414.19        文献标识码:A

        卫星帆板中广泛应用蜂窝夹心结构,主要是以蜂窝芯层为基础,分别在其上下表面粘贴复合材料蒙皮而成[1]。以蜂窝夹层板作为卫星帆板的主体结构, 当帆板受到冲击载荷时, 蜂窝芯体、上下蒙皮和胶层可以吸收大量能量。相当于在电池阵和冲击源之间设计了一个低频单自由度系统,形成一个低通滤波器,从而通过缓冲结构的变形吸收高频冲击载荷的能量。同时由于面板和蜂窝芯层的材料不同,界面的机械阻抗不匹配,使冲击波过界面时发生反射而降低冲击的能量。因此,蜂窝夹层板很好的综合了柔性吸能法和刚性隔离法的优点, 能满足结构的强度和安装精度要求。

建立精准的卫星帆板限元模型是比较困难的,在建模过程中会受到诸多因素的干扰。蜂窝板模型的等效理论方法、各结构之间的连接关系、材料属性的定义以及有限元网格的质量等因素都会影响到有限元模型的精度, 造成有限元模型与真实卫星帆板产生偏差。为了保证最终分析结果的准确性,有必要对所搭建帆板模型的 准确性进行评估。而相关性分析就是分析实验测试和仿真分析之间误差的有效方法。在满足一定可靠性的前提下可认为模态试验测试的数据为准确结果, 通过仿真与试验对比分析来验证模态计算结果正确与否。只有当MAC值在可接受的范围内时,才能认为有限元模型准确, 才可以利用该仿真模型为后续的产品设计开发工作 进行深入分析[2]。

        本文针对单块卫星帆板结构建模方法的正确性进行相关性分析,采用三明治夹芯板理论建立了一种芯层均匀壁厚正六边形帆板有限元模型进行模态分析,通过把模态仿真结果与模态试验测试数据进行相关性分析,验证了卫星帆板建模方法的正确性,从而确保卫星整体分析结果的准确性[3,4]。

1 数值模型建立

        以往蜂窝夹层结构建模时,芯层的面内刚度和弯曲刚度经常被略掉,通过对比发现数值分析结果与试验测试数据存在一定偏差。造成这样结果的主要因素是面内刚度和弯曲刚度的缺失引起的。虽然蜂窝芯层刚度比较低, 但相对于蒙皮而言仍具有较大的厚度, 因此这两个参数对分析结果仍有一定的影响, 不应被忽略掉。

        三明治夹芯板理论等效方式主要是以芯层为等效对象。假定芯层能抵抗横向剪切, 同时具有一定的面内刚度, 上、下面板层符合小挠度薄板的Kirchhoff假设, 则蜂窝芯层可以等效为一均质的厚度不变的正交异性层 [5,6,7]。图 1为蜂窝夹层板的几何参数, 图中a为蜂窝夹层 板的板长, b为板宽, hf为上下面板厚度; hc为芯层厚 度;t为蜂窝芯壁厚;L为边长。对应正六边形蜂窝芯层等

效材料参数可以通过式 (1) 进行计算获取。

图 1 蜂窝夹层板的几何参数

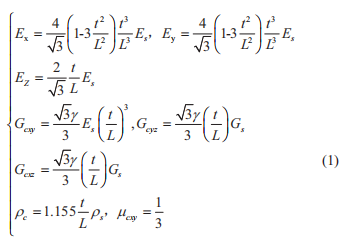
式中, E, P, P, μ 分别是弹性模量、剪切模量、密度、泊松比, 其中下角标为s表示蜂窝芯层弹性参数, 角标为c表示等效芯层的弹性参数。Y为修正系数, 一般取0.4-0.6。

        运用等效参数公式 (1) 获取的材料参数如表1中铝蜂窝所示, 通过芯层的各等效参数、边框和面板参进行卫星帆板建模和仿真分析。

                                     表一 蜂窝板几何与材料参数

        卫星帆板的有限元模型在Hypermesh中建立, 该模型主要包括三明治夹层结构、边框和帆板固定基座三部分,如图2所示。卫星帆板固定基座采用铝合金材料,边框以及蜂窝板上下蒙皮结构采用碳纤维铺层而成,复合材料有各向异性的特点,可以对铺层的顺序、角度以及比例等条件进行设计,来满足不同的结构的力学要求,  从而最有效的发挥材料的作用[8]。在有限元建模过程中, 使用壳单元进行模拟, 单元基本尺寸为10mm,并用 pCOMpG卡片进行铺层定义, 具体铺层定义如表2所示。为保持过渡区表面光顺变化平缓,每次铺层递减不超过2层, 再次铺层递减需隔开一定距离[9] 。固定帆板的四处螺栓连接使用RBE2单元模拟。有限元帆板模型共包括432145个节点和425390个单元。

                 表二 帆板铺层参数

图 2 卫星帆板有限元模型

2 模态数据获取

        在帆板设计前期阶段,通过计算模态分析可以帮助 确定测试中测点的位置分布,以及参考点的位置; 在后期阶段,试验测试结果可以帮助校准帆板有限元模型, 提高分析精度, 二者相辅相成。

2. 1 仿真模态分析

        对卫星帆板进行模态分析,了解和掌握其动力学特性是考察产品动态特性的基础[10]。在线性时不变条件下, 实际连续的非线性物理结构可离散为一个具有N自由度的线性弹性系统,描述系统的运动的微分方程如式2所示,通过求解该方程可以得到系统的固有频率和振型。

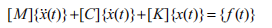  (2)

        其中,[M]为质量矩阵, [C]为阻尼矩阵, [K]为刚度矩阵, {X}为特征向量,{f(t)}为外部激振力。

        将处理好的卫星帆板有限元模型提交到MSC. NASTRAN进行模态分析得到四角约束状态下的帆板板前六阶模态。根据模态有效质量理论,模态分析重点关注第1阶弯、扭等整体模态频率,其前两阶振型如下图3所示。蜂窝板有限元的前六阶模态结果如表3所示。

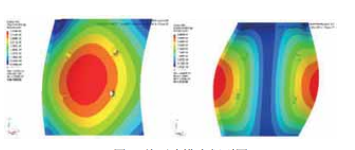
图 3 前两阶模态振型图 

            表三 仿真分析结果

2. 2 试验模态测试

        模态测试是根据试验测得频响函数矩阵或脉冲响应函数矩阵, 采用模态参数估计方法求出结构的模态参数。只通过测量结构的输入和输出计算出频响函数, 不测量结构的质量和刚度。

        频响函数的分子为留数与模态振型有关,分母包含极点信息与模态的频率与阻尼有关。 因此通过测量结构的频响函数可以测得系统的全部模态信息, 频响函数如式3所示。

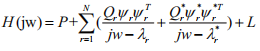      (3) 

        其中,r表示阶数,中间项为分析频带内的模态, 但实际上在分析频带范围外还存在上残余项P, 下残余项L。

        进行模态测试系统主要包括数据采集前端、B&K8206 型力锤、B&K 4524 型加速度传感器、计算机。利用模态测试系统对蜂窝板进行模态试验,试验测点布置如图3所示。运行PULSE Front End Setup前端, 打开MTC Hammer模块进行设置。在整个帆板上布置16个测点,为了保证试验数据的一致性,采用单点激励多点输出方式进行测试。以第9点为激励点进行激励,可以同时测得16个响应点3个方向的振动加速度响应,保证了 各点测试结果的一致性,拾取蜂窝板350Hz以下的振型,  模态测试分析的采样频率为1024Hz, 采样时间为1s,其实际测试布点位置如图4所示。

图 4 模态测试响应点

        根据实测的激励信号和响应信号, 按照 Hv法来估计频响函数矩阵,在感兴趣的频率范围内借助稳态图识别系统极点, 再利用最小二乘频域法估计振型,得到蜂窝板的前六阶实验模态振型。蜂窝板有限元模态计算的具 体结果如表4所示。

              表四 模态试验结果

3 模态相关性分析

        运用相关性分析来判断试验测试与有限元模的型符合程度判断出有限元建模的准确性具有极强的工程意义。固有频率通常是动力学分析中最基本的参数,而且比模态向量更容易准确测量,测量频率fT与计算频率fA之间的误差通常以式4表示。

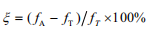                (4)

        振型符合度分析是一个重要的参数,可以帮助判断测量与计算模态之间的对应关系,只有在振型一致的情况下的进行的频率符合度分析才是可靠的。通常采用模态置信度MAC来评估模态振型的符合程度,计算公式如式5所示。MAC通过比较试验模态向量与分析模态向量间的线性相关性来判断各阶模态的置信度。当MAC=1时, 表明2个模态向量完全线性相关, MAC=0时, 表明2 个模态向量线性无关。

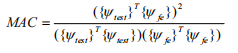        (5)    

式中:  {Ψtest } 为试验模态振型向量  {Ψfe }为有限元模态振型向量

        由于帆板有限元模型的节点数远高于试验测试模型节点数目, 所以有限元模型和试验模型节点自由度数量不相容。因此需要将试验模型所有的节点映射到有限元模型上进行匹配, 找到试验模型节点对应的有限元节点, 得到缩减的有限元模型,从而建立有限元模型和试验模型之间的关联。将帆板有限元原模型模态矩阵做等效处理,传递到缩减的有限元模型上,最终通过对实验模态振型和缩减的有限元模型进行相关性分析即可得到图5所示的模态置信度MAC矩阵。对卫星帆板进行频率符合度和振型符合度分析,可以得到频率相关性和振型符合度结果, 如表 5 所示。

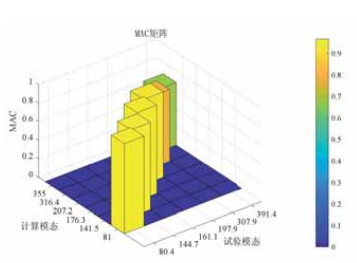
图 5 MAC 矩阵

           表五 频率符合度和振型符合度

        表5列出了帆板前6阶实验模态和计算模态的比较,从表中可以看出200Hz以内的前四阶模态振型MAC值均在0.9以上,振型符合度满足工程参考及分析要求值0.8 , 满足工程中对于模态相关性值的要求。总体看来, 蜂窝板的实验和仿真分析的固有频率和振型二者能比较好地吻合。进一步分析,由于计算模态与实验模态阻尼设定的区别、试验模态过程中数据采集过程中的误差、计算模型与物理模型的差异等因素影响,导致计算模态和实验模态的差异性。

4 结论

        本文以卫星帆板结构为研究对象, 运用三明治夹芯板理论建立了一种卫星帆板的有限元模型,在此基础上进行了模态分析,然后将分析结果与模态测试数据进行相关性分析。 由分析结果可以看出, 模态的仿真计算与试验测试结果频率和振型的一致性保持良好, 前四阶MAC值到达0.9以上。验证了该种卫星帆板有限元模型的精度,能够很好的模拟原模型的动力学特性,在此基础上以有限元模型代替试验模型进行深入分析,对整星动力学进一步的研究具有重要的借鉴和指导意义。

参考文献:

[1]    夏利娟,  金咸定,  汪庠宝.  卫星结构蜂窝夹层板的等效计算[J].  上海交通大学学报, 2003(07): 999-1001.

[2]    张松波,  周建文.  基于 LMs Virtual.Lab 的汽车模态相关性分析与优化[J].  汽车技术, 2010(07): 16- 19.

[3]    郝鸿雁,  黄志亮.  蜂窝板结构等效弹性模量的测试[J].   中国测试, 2013, 39(01): 121-124.

[4]    付立英,  王维扬.  卫星用蜂窝夹层板的等效计算及实验研究[J].  科学技术与工程, 2008, 8(23): 6429-6432.

[5]    张铁亮,  丁运亮,  金海波.  蜂窝夹层板结构等效模型比较分析[J].  应用力学学报, 2011, 28(03): 275-282+327.

[6]    Li shi-qiang, xin Li, Wang zhi-hua, Wu Gui-ying, Lu Guo-xing, zhao Longmao. Finite element analysis of sandwich panels with stepwise graded aluminum honeycomb cores under blast loading[J]. Composites partA, 2016 , 80 :  1-12.

[7]    Y. Tanimoto, T. Nishiwaki, T. shiomi & z. Maekawa. A numerical modeling for eigenvibration analysis of honeycomb  sandwich panels[J]. Composite Interfaces, 2012, 8(6):393- 402.

[8]    沈观林,  胡更开.  复合材料力学[M].  北京:  清华大学出版社, 2006.

[9]    冯雁,  郑锡涛,  吴淑一.  轻型复合材料机翼铺层优化设计与分析[J].  航空学报, 2015, 36(06): 1858-1866.

[10]  马炳杰,  冯慧华,  廖 日东,  姚利民. 基于模态相关性和模型修改的发动机整机模态分析[J].  车辆与动力技术, 2006(02):

38-42+64.